Fig. 1 Pont du Gard side view (photo P. Hunt, 2015)
By David S. Spain, Ph.D. –
One of the favorite examples of Roman aqueduct technology is the famous Pont du Gard in southern France. The arcaded Pont du Gard is part of the 50 km long aqueduct from springs near Uzes running all the way to Nimes (the Roman colony of Nemausus). The aqueduct was apparently finished in the first century CE, although possibly planned even earlier under the supervision of famous Roman administrator and engineer Marcus Agrippa who visited Nimes since some of the aqueduct trenches and tunnels are likely from the first century BCE.[1] Although Nimes is only 20 km in a direct line from Uzes as the crow flies, a circuitous route was required to skirt the southern foothills of the Massif Central and avoid steep gradients, maintaining a gradient of around 2% as much as possible partly to reduce the spring season volume of water into Nimes.[2] The Pont du Gard was built to allow the aqueduct to cross the Gardon River. It was originally 360 m long and 49 m high and consists of three layers of arches built in locally quarried limestone blocks without a single nail or spike and without any cement.[3] The significant amount of greater open space than filled space in this design helps to reduce wind forces, and large piers on the lowest level provide resistance to water pressure with v-shaped water splitting shapes facing the water flow when the river is high, also reducing water force against the stone. The lowest level of arches is 22m high, the second level is 20 m high, and the uppermost level is 7 m high. In spanning the east-west flowing Gardon River by crossing it from north to south, the aqueduct carried by the Pont du Gard descends only 2.5 cm over 900 feet of the aqueduct spanning the river – an indication of the precision of Roman engineering, which can also be detailed in looking up into one of the aqueduct large arches with exact numbering of stones (Figs. 2a & 2b).
Fig. 2a Pont du Gard Arch Numbering (Photo P. Hunt, 2015)
Fig 2b Pont du Gard Arch Numbering (image in public domain)
The Pont du Gard is familiar to archeologists and makers of tourism posters. Less well known is that so many blocks of the arches in the aqueduct are labeled with both the level and position (Fig. 3) including front, left, center, middle, right (front facing or facade = FR frons, left = S sinister , right = D dextra, middle = M medium or coded in similar abbreviations).
Fig. 3 Close-up detail of Pont du Gard Arch Numbering (image in public domain)
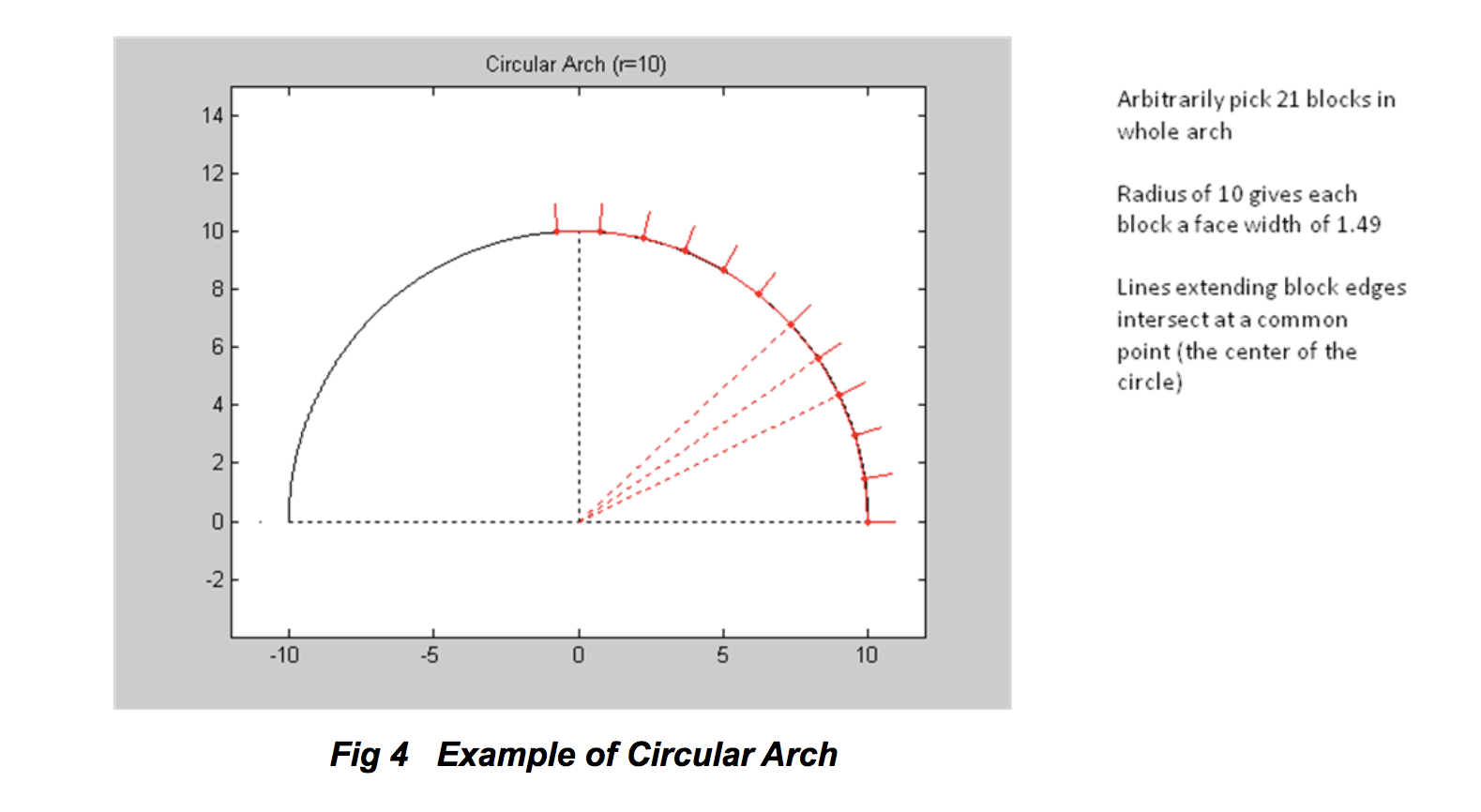
Once we see this labeling, the natural question is to ask why? If all the arches were circular, all blocks of the arch would be identical and no specific stone labeling would be needed. The blocks would be regular trapezoids, where the angles between the face of the blocks and its two sides would be equal and would be the same for every block. The figure below (Fig. 4) shows a circular arch 20 units in width and 10 units in height (pick whatever units you like). For ease of illustration, we have chosen hypothetically an arch with 21 blocks in the whole arch, with the face of the keystone the same width as all the other blocks. This choice results in blocks whose face is 1.49 units wide, where the angle between the face and side of the block is 94.29 degrees. We can also see that when the lines between the sides of adjacent blocks are extended (the dashed red lines); they all meet at the center of the circle. The arches on the middle level of the Pont du Gard have three times the number of blocks, but the principle is the same. For a circular arch, all of the blocks would be identical (and hence interchangeable) and there would be no need for labeling.
(Schematic of David S. Spain, Ph.D.)
Now suppose instead of a fairly perfect circular arch, we choose an elliptical arch. Consider an arch where the parabolic height is greater than half the width. Again for ease of illustration, we hypothetically pick an arch 18.82 units high and 20 units wide, with blocks of face width approximately the same width as before (1.47 units). This choice results in 31 blocks in the whole arch, 15 on each side plus the keystone (the block face width, the number of blocks, and the height of the arch cannot be chosen independently). As with the circular arch, we assume that the common side between two adjacent blocks is the bisector of the angle between the two faces. With this arch, the angles between the block face and the block edge vary from 91.21 to 97.75 degrees – not a huge amount but certainly not interchangeable. This arch is illustrated below (Fig. 5). Notice that the angles between the face of the block and its two sides are not quite the same, and the extensions of the lines of the faces no longer intersect the centerline of the arch at a single point.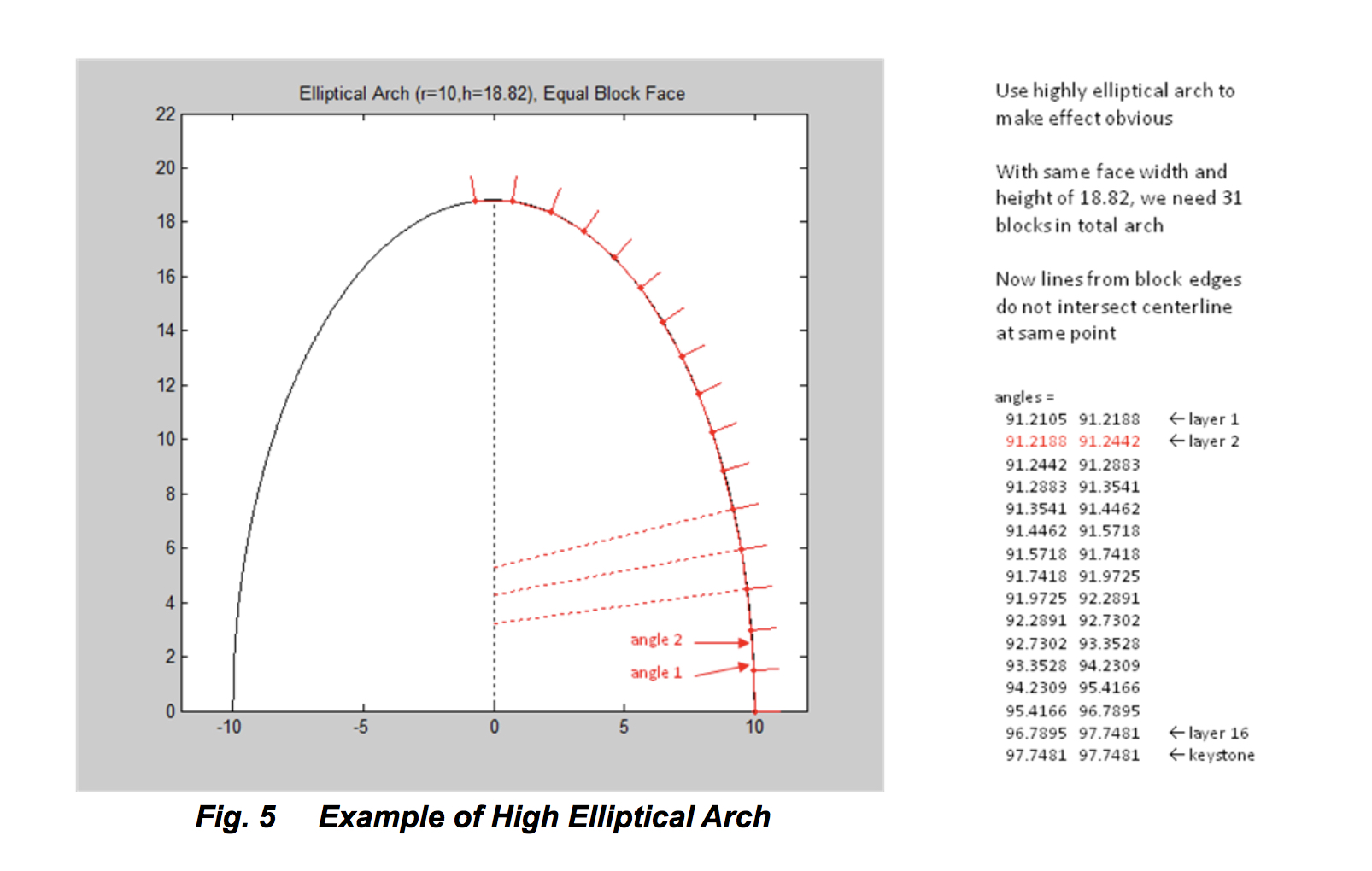
Schematic of David S. Spain, Ph.D.)
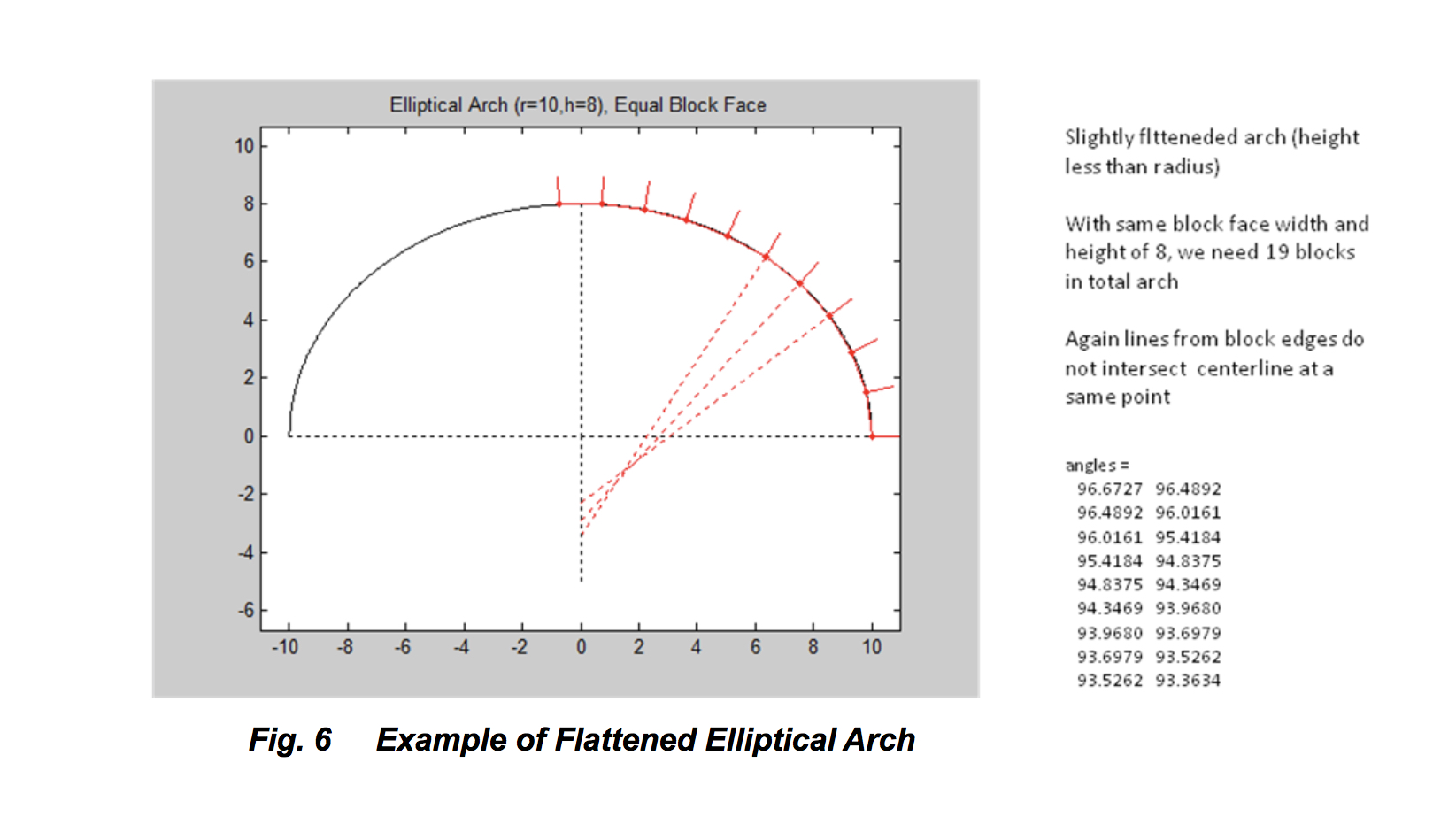
Now finally hypothetically consider an elliptical arch where the parabolic height is less than half the width (Fig. 6). With an arch 8 units high and 20 units wide and the same block face width (1.49 units), we need 19 blocks in the whole arch. Again, the angles between face and edge vary from block to block and the extensions of the lines of the faces do not intersect the centerline of the arch at a single point.
(Schematic of David S. Spain, Ph.D.)
When we look straight on at the side view of the Pont du Gard below, we notice that the arches in the lower level definitely appear to be flattened (the height less than half the width) relative to the spring level of the arch where the voussoirs [4] (wedged arch block stones) start. The first large arch on the second tier even has a different spring level than its adjacent pier. The first several arches in both the first and the second level also appear to be flattened to a lesser extent.
Fig. 7 Pont du Gard side view (photo P. Hunt, 2015)
While these observations are not conclusive, they do provide a possible reason for labeling each block in the arch with its level and position. The blocks were undoubtedly carved and fitted off-site and then assembled on-site, but even so, the most stable configuration would be for the common side between two blocks to be angle bisector of the two faces. In conclusion, Roman engineers may have numbered the stones from the prepared model already knowing the necessarily flattened parabolas that made it possible for the open space (60%) relative to the closed space (40%) to be greater for lowering wind resistance in high winds, which also suggests Roman engineering understood some sort of vector analysis. Whether or not the rationale offered here is provable or observable elsewhere, Roman engineering continues to surprise even into the 21st century.
Editor’s Note: the author, who has a Ph.D. in Engineering from Stanford following his B.S. and M.S. from the same institution, worked with Patrick Hunt, Ph.D. in Archaeological Science from the Institute of Archaeology, UCL. Hunt posed the question in a Stanford post-grad course, HIS 122 Ancient Engineering that Hunt taught in fall of 2018.
Notes:
[1] Donald Hill. History of Engineering in Classical and Medieval Times. Routledge, 1996, 70, also illustrated 260.
[2] Guilhem Fabre, Jean-Luc Fiches, Jean-Louis Paillet, Jean-Louis. “Interdisciplinary Research on the Aqueduct of Nimes and the Pont du Gard”. Journal of Roman Archaeology 4 (1991) 63-88.
[3] Andrew Wilson in J. P. Oleson, ed. Oxford Handbook of Engineering and Technology in the Classical World. Oxford, 2008, ch. 11, 299.
[4] J. G. Landels. Engineering in the Ancient World. Berkeley: University of California, 1978, 41-2.