By Douglas McElwain –
Inca measurements are systematic as they apply to architecture and quipu knot structures. This article suggests a relationship between three seemingly disparate elements of Inca culture; stone walls, distance units of measure, and quipu (surviving string knot artifacts).
Walls
The Inca of Peruvian South America lived in a geologically active zone with frequent and powerful earthquakes along the Andes Mountain chain. The unique characteristics of the Inca architecture are likely the result of their experience with these earthquakes and the engineering solutions they developed to mitigate the earthquakes’ destructive effects. The Inca solutions, sometimes in concert and sometimes alone, exhibit a high degree of engineering skill. This in turn implies precision in their construction processes.
Many Inca walls have a sloping or trapezoidal cross section (a 3 to 5 degree batter). This means less weight at the top of the wall thereby making the center of gravity lower which in turn makes the wall more stable and resistant to shaking. Rounded corners where walls came together minimize concentrations of stress during earthquakes. Irregular shaped blocks lock the blocks together. Lastly, the blocks in the Inca walls fit so tightly together that a knife blade cannot be slipped between them. However, this slight separation reduces the transmission of forces through the walls and gives the walls flexibility thereby improving their resistance to earthquakes.

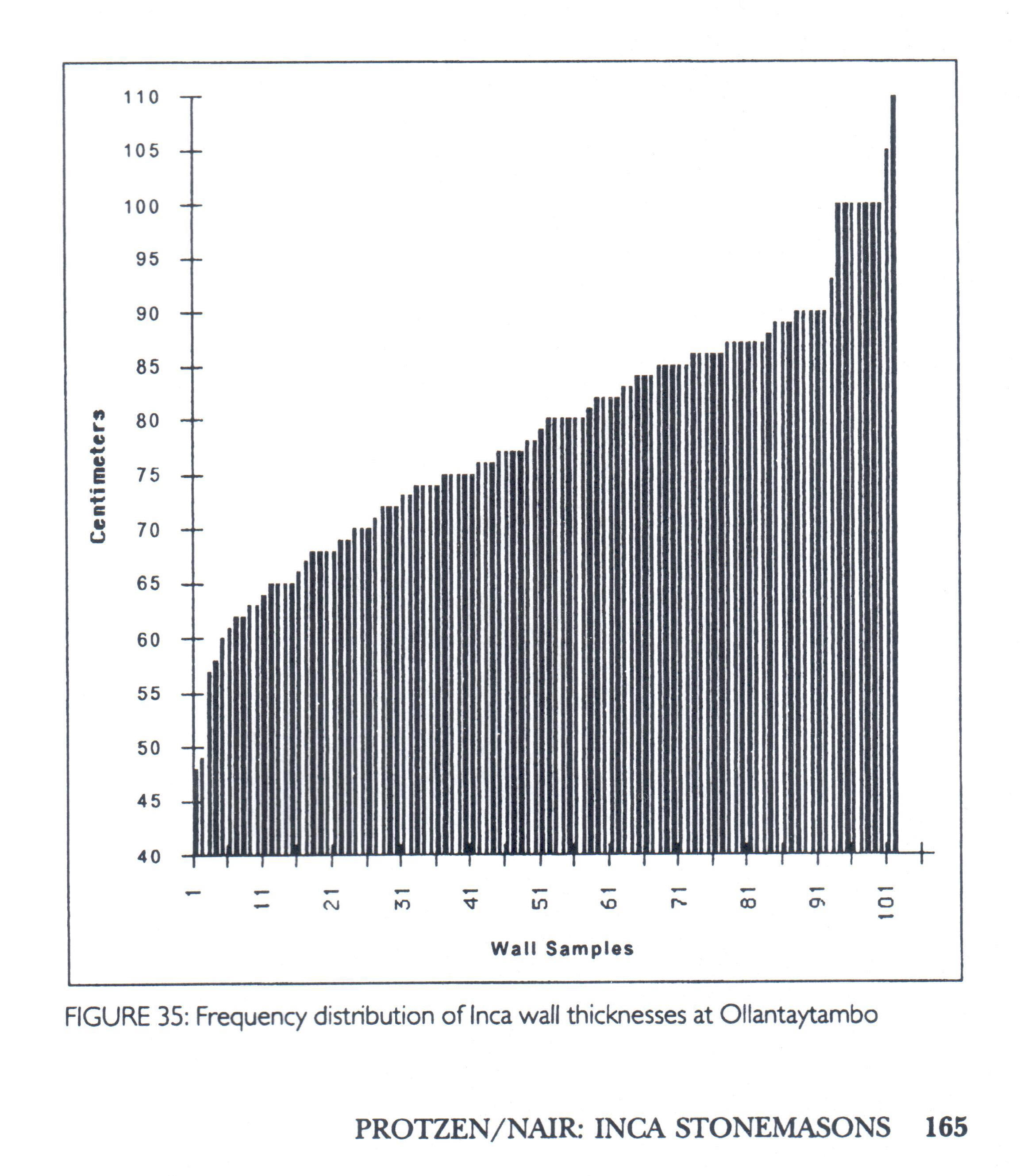
Based on the techniques the Inca developed to mitigate the damage caused by earthquakes one would expect that the thickness of their walls might be important. However, except for a minimum distance, wall thickness seems to vary widely (see the figure below for the walls at Ollantaytambo) (1) It is possible that wall thickness is more closely related to the overall size of the structure or the newness of construction (representing something analogous to improved building codes).
Distance Units of Measure
As John Rowe said some years ago, Information on Inca units of measurement is relatively abundant, but so scattered and unsystematized as to give the impression that the Inca had no very precise standards. Actually Inca skill in engineering works almost required a system of measurement at least as exact as that in use in 16th-century Europe. (2) Therefore it is very likely the Inca used some type of standardized units to measure distances.
The current belief is that the length of the distance units is based on the human body. However, this is unlikely to produce standardized distances. Body sizes differ between people which in turn create variable units of distance. This is inconsistent with the precision needed for the demonstrated construction. It is possible the Inca distance units based on the human body came about because the Inca used rule-of-thumb measures in less demanding, everyday situations. Below are the known Inca units of distance:
Inca Word Description for Distance
rikra (3) Distance of a man’s outstretched arms (4) = 162 cm (5)
sikya (6) = One half rikra. (7) = 81 cm (8)
khococ (9) Distance from elbow to tip of the hand (10) = 45 cm (11)
kâ’apa (12)= Size of a palm (13)= 20 cm (14)
yuku (15) = Tip of outstretched thumb and forefinger (16) = 10 cm (17)
One characteristic to note about the units of distance above is that they appear to form a geometric progression. Starting at the rikra each successive unit is half the previous one (the exception to this is the khococ which is about 12% off). Gary Urton, referring to a unit of measure for land area called the tupu (different from the Inca unit of distance with the same name discussed later), stated that:
Gonzalez Holguan notes that half of huc tupu (one tupu) as the unit called checta; one-quarter of a tupu was the sillcu; and one eighth was the cutmu. Thus the normative principle of partitioning tupus as reflected in this terminology was the full tupu unit successively halved, a process that reflects what was perhaps the most common organizational principal in the Inka state: dualism, or the (repetitive) subdivision of whole units into halves.(8)
Therefore, I propose that the Inca applied the same halving principle to their distance units of measure. If the halving principle is correct and applied to the length of the rikra in the previous table, the units of distance would be:
rikra 162 cm
sikya 81 cm
khococ 40.5 cm
kâ’apa 20.25 cm
yuku 10.125 cm
This table is based on the assumption that the rikra is the most reliable of the Inca distance measurements. The Spanish called the rikra the fathom. The fathom was the standard measurement of land, and a measuring stick (CQTA-KâASPI) of this length was kept as a legal check.(9) This series of distances would support precise construction planning because it is based on the standard Inca measuring stick.
It would not be unreasonable for this series of measurement units to extend further in both directions (see Table at end of article). If it did, a tupu (measure of distance) would be 6.6 km versus 7.3 km estimated by Rowe (20) and 7.8 km reported by McEwan. (21) However, there appear to be enough uncertainty as to the actual length of a tupu to make this worthy of additional study.
Protzen was unable to relate the wall thicknesses graphed above to Inca units of measure. (22) However, another analysis of the wall thickness (23) data should be performed in order to determine if wall thickness can be described by choosing particular terms from the proposed series.
For example, the bar on the far right in the above graph appears to be about 110 cm in length. It could be explained by adding one sikya plus one kâ’apa plus one yuku as illustrated in the following table.
yuku k’apa khococ sikya rikra Total
Std. length (cm) 10.125 20.25 40.5 81 162
Number of combined units 1
Total cm 10.125 20.25 81 111.37
By making this calculation for each wall the applicability of this approach could be tested. In addition it might be possible to discover additional terms (standard lengths) in the series.
It should be noted that the Aztec standard unit of distance (also believed to be based on the human body) has been proposed by various researchers to be 80.0 cm, 80.5 cm, 82.5 cm and 83.0 cm. (24) While the similarity of the length of the Inca sikya to the Aztec measurement unit is not evidence of a common derivation or interaction between the two cultures, it seems very coincidental and therefore worthy of further study.
Quipu (or Khipu)

It is accepted that quipus are a medium for record storage. Information storage beyond records however is speculation because quipus have not been fully deciphered. However, as Urton describes them,
Khipus are knotted-string devices made of spun and plied cotton or camelid fiber. The colors displayed in khipus are the result of the natural colors of cotton fiber and camelid hair or of the dyeing of these materials with natural dyes. The backbone of a khipu is the so-called primary cord, a ca. 0.5 cm in diameter cord which are attached to a variable number of thinner strings, called pendent cords. … Khipus contain from as few as one up to as many as 1,500 pendants. … The majority of khipus have knots tied into pendant, subsidiary, and top strings in tiered clusters in a decimal system of numeration (Locke 1923). Three basic type of knots make up the decimal signing system … While roughly two-thirds of all khipus studied to date have their knots organized in the decimal manner described, about one-third of the samples bear knots scattered across the cords in a non-clustered, non-tiered fashion. 5)
Therefore, while speculative, quipus are believed to hold non-decimal information.
Intersection
The previous discussion leads to the hypothesis that quipus could record the geometric progressions necessary to measure the thickness of building walls. The Inca knew about the number zero. In turn it has been proposed that the lack of a knot on a pendant position could signify a zero value for that item. (26) Additionally, multiple knots at an appropriate position could signify multiple values for that item.
As an example, look at the table above. Instead of the description ˜Number of Units”, replace it with ˜Number of Knots”. A quipu could easily be used to represent this value (i.e., in this example a pendant would have five positions; some filled, some unfilled – one knot [1st position], one knot [2nd position], no knot [3rd position], one knot [4th position], no knot [5th position]).
More broadly, the quipu could have been used to hold the dimensions of buildings under construction. A schematic if you will. Individual pendants could hold the parameters for wall length, height, thickness at the top and thickness at the bottom. Assuming each wall is defined by these four parameters, sixteen pendants would be needed to represent the layout of the outer walls of a rectangular building (not including information for doors and windows).
One question that arises from this approach is how the Inca calculated the width at the top of the wall and the width at the bottom of the wall to achieve a 3 to 5 degree wall batter. This angle range translates into a distance of 8.5 cm and 14.2 cm per 162 cm rikra. This two degree batter range suggests a rule of thumb technique as opposed to a more precise mathematical one.
Given the small number of quipus surviving – estimated to be over 750 (27) – it would be unlikely that a quipu exists that matches an existing Inca building or ruins. Not impossible, just unlikely. Still, it might be worth searching those un-deciphered quipus mentioned above by Urton in order to determine if the patterns of knots on the pendent cords match building dimensions.
| Table: |
Hypothetical Inca Units of Distance Measurement |
|||||
|
(based on the rikra) |
||||||
|
km to mile = |
0.621371 |
|||||
|
Modeled Distances |
||||||
|
Inca Unit |
(Rowe) | (McEwan) |
cms |
meters |
kms |
miles |
|
? |
0.6328125 |
|||||
|
? |
1.265625 |
|||||
|
? |
2.53125 |
|||||
|
? |
5.0625 |
|||||
|
yuku |
12-14cm |
10.125 |
0.1 |
|||
|
k’apa |
20 cm |
20 cm |
20.25 |
0.2 |
||
|
khococ |
45 cm |
45 cm |
40.5 |
0.4 |
||
|
sikya |
81 cm |
81 cm |
81 |
0.8 |
||
|
rikra |
162 cm |
162 cm |
162 |
1.6 |
||
|
unknown ? |
324 |
3.2 |
||||
|
unknown ? |
648 |
6.5 |
||||
|
unknown ? |
1,296 |
13.0 |
||||
|
unknown ? |
2,592 |
25.9 |
||||
|
unknown ? |
5,184 |
51.8 |
0.1 |
|||
|
unknown ? |
10,368 |
103.7 |
0.1 |
|||
|
unknown ? |
20,736 |
207.4 |
0.2 |
|||
|
unknown ? |
41,472 |
414.7 |
0.4 |
|||
|
unknown ? |
82,944 |
829.4 |
0.8 |
|||
|
unknown ? |
165,888 |
1,658.9 |
1.7 |
1.0 |
||
|
unknown ? |
331,776 |
3,317.8 |
3.3 |
2.1 |
||
|
 tupu |
~7.2km |
7.8km |
663,552 |
6,635.5 |
6.6 |
4.1 |
|
unknown ? |
1,327,104 |
13,271.0 |
13.3 |
8.2 |
||
|
unknown ? |
2,654,208 |
26,542.1 |
26.5 |
16.5 |
||
|
unknown ? |
5,308,416 |
53,084.2 |
53.1 |
33.0 |
||
|
unknown ? |
10,616,832 |
106,168.3 |
106.2 |
66.0 |
||
|
wamami |
~216 km |
234km |
21,233,664 |
212,336.6 |
212.3 |
131.9 |
Note: One reference lists the tupu (spelled topo) as either 4.5 miles or 6.0 miles – depending on the authority cited.(8)
In conclusion, Inca measurements replicate their units by doubling from the smallest unit or halving from the largest units, so the systematic approach taken here is not so theoretical as it is building from the known to the unknown. In future, Quechua linguistics may not be able to fill in all the gaps as easily as logic dictates, but the units for both quipu knots and architectural dimensions of walls and distances might be argued fairly persuasively as this article surmises.
Bibliography
Malpass, Michael Andrew. 2008. Daily Life in the Inca Empire. Indianapolis, IN: Hackett Publishing Company, Inc.
McEwan, Gordon F. 2008. The Incas: New Perspectives. New York, NY: W. W. Norton & Company.
Protzen, Jean-Pierre and Stella Nair. June 1997. “Who Taught the Inca Their Skills: A Comparison of Tihuanaco and Inca Stone-Cut Masonry,” volume LVI, No. 2. Journal of the Society of Architectural Historians. Chicago, IL: Society of Architectural Historians.
Rowe, John H. 1946. “Inca Culture at the Time of the Spanish Conquest,” Handbook of South American Indians, vol. 2, ed. Julian H. Steward; Washington, D.C.: Smithsonian Institution.
Urton, Gary. 2010. “Recording measure(ments) in the Inka Khipu,” The Archaeology of Measurement: Comprehending Heaven, Earth and Time in the Ancient Societies. Iain Morley and Colin Renfrew; Cambridge, UK: Cambridge University Press.
Notes
1 Protzen, Jean-Pierre and Stella Nair. June 1997. “Who Taught the Inca Their Skills: A Comparison of Tihuanaco and Inca Stone-Cut Masonry,” Volume LVI, No. 2. Journal of the Society of Architectural Historians. Chicago, IL: Society of Architectural Historians, 165.
2 Rowe, John H. 1946. “Inca Culture at the Time of the Spanish Conquest,” Handbook of South American Indians, vol. 2, ed. Julian H. Steward; Washington, D.C.: Smithsonian Institution, 323.
3 Protzen and Nair, 1997, 165.
4 McEwan, Gordon F. 2008. The Incas: New Perspectives. New York, NY: W. W. Norton & Company, 220.
5 Protzen and Nair, 165.
6 Ibid.
7 McEwan, 220.
8 Protzen and Nair, 165.
9 McEwan, 215.
10 Ibid.
11 Ibid.
12 Rowe, 323.
13 McEwan, 215.
14 Rowe, 323.
15 Ibid.
16 Ibid.
17 Hunt, Patrick. February 14, 2015, response to a Stanford University ARC 122 Canvas General Questions and Comments question.
18 Urton, Gary. 2010. “Recording measure(ments) in the Inka Khipu,” The Archaeology of Measurement: Comprehending Heaven, Earth and Time in the Ancient Societies. Iain Morley and Colin Renfrew; Cambridge, UK: Cambridge University Press, 56.
19 Rowe , 323.
20 Ibid, 323-324.
21 McEwan, 222.
22 Protzen and Nair, 165.
23 Ibid.
24 Sugiyama, Saburo. 2010. “Teotihuacan city layout as a cosmogram,” The Archaeology of Measurement: Comprehending Heaven, Earth and Time in the Ancient Societies. Iain Morley and Colin Renfrew; Cambridge, UK: Cambridge University Press, 133-134.
25 Urton, 55.
26 Rowe, 326.
27 Urton, Â 55.
28 Malpass, Michael Andrew. 2008. Daily Life in the Inca Empire. Indianapolis, IN: Hackett Publishing Company, Inc., 96.